四年级运算定律公式全面释义、解释与落实
在四年级的数学学习中,运算定律是数学基础中的基础,它不仅帮助学生理解数学运算的规律性,还为后续的数学学习打下坚实的基础,四年级学生需要掌握的八大运算定律包括:加法交换律、加法结合律、乘法交换律、乘法结合律、乘法分配律、减法性质、除法性质以及括号的作用,本文将全面释义这八大定律,并探讨如何在教学中有效落实这些定律。
加法交换律与结合律
释义:
- 加法交换律:两个数相加,交换加数的位置,和不变,即a + b = b + a。
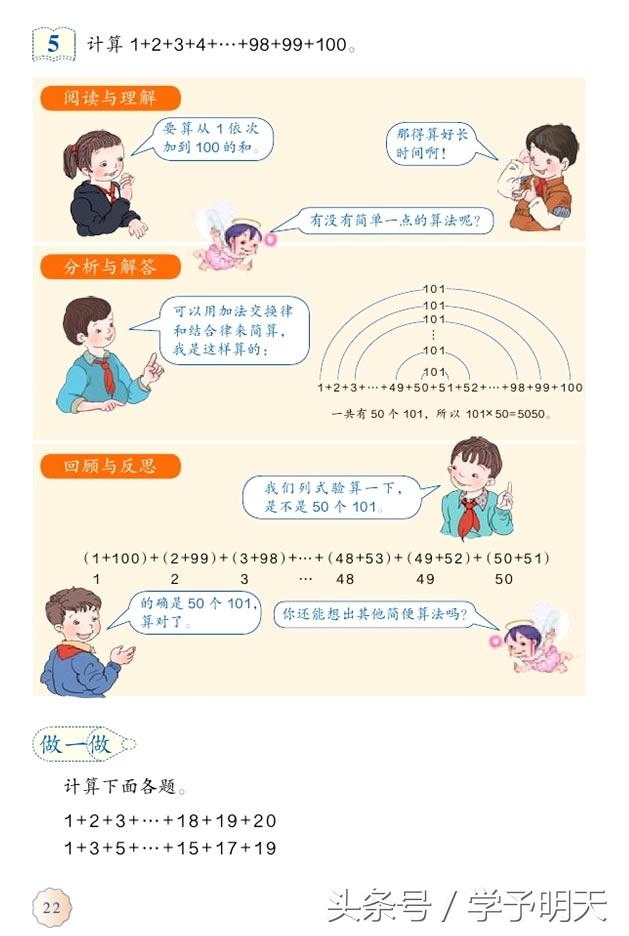
- 加法结合律:三个或更多数相加,可以先把前两个数相加,或者先把后两个数相加,和不变,即(a + b) + c = a + (b + c)。
解释: 加法交换律和结合律是数学中最基本的运算规律之一,它们帮助学生理解加法的灵活性,即加法的顺序可以任意改变而不影响结果。
落实方法:
- 实物操作:使用小木棍或豆子等实物进行加法运算,通过变换加数的位置或组合方式来直观展示交换律和结合律。
- 游戏化教学:设计“数字接龙”等游戏,让学生在游戏中体会加法的交换性和结合性。
- 应用题:创设生活情境,如购物找零问题,让学生在解决实际问题中运用加法交换律和结合律。
乘法交换律与结合律
释义:
- 乘法交换律:两个数相乘,交换乘数的位置,积不变,即a × b = b × a。
- 乘法结合律:三个或更多数相乘,可以先把前两个数相乘,或者先把后两个数相乘,积不变,即(a × b) × c = a × (b × c)。
解释: 乘法交换律和结合律是乘法运算的基本规律,它们展示了乘法运算的灵活性,即乘法的顺序可以任意改变而不影响结果,这对于培养学生的逻辑思维和数学直觉非常重要。
落实方法:
- 实物模型:利用面积模型或长度模型来展示乘法交换律和结合律,帮助学生直观理解。
- 互动讨论:组织学生进行小组讨论,通过实例分析来加深理解。
- 应用题:设计涉及连续乘法的问题,如计算连续几天的总收入等,让学生在解决实际问题中运用乘法交换律和结合律。
乘法分配律
释义:两个数的和与一个数相乘,等于这两个数分别与这个数相乘的和,即(a + b) × c = a × c + b × c。

解释: 乘法分配律是四年级数学中的重点和难点,它展示了乘法与加法之间的内在联系,是数学运算中的重要工具,掌握乘法分配律有助于简化复杂计算,提高运算效率。
落实方法:
- 直观演示:利用面积模型或分组法来展示乘法分配律的直观过程。
- 分步练习:设计分步计算的练习题,逐步引导学生理解并应用乘法分配律。
- 实际应用:创设购物、分配任务等生活情境,让学生在解决实际问题中运用乘法分配律。
减法性质与除法性质
释义:
- 减法性质:连续减去两个数等于减去这两个数的和,即a - b - c = a - (b + c)。
- 除法性质:连续除以两个数等于除以这两个数的乘积(在除数不为零的情况下),即a ÷ b ÷ c = a ÷ (b × c),但需注意,这里的除法性质在实际应用中较为特殊,通常更强调减法和除法的逆运算关系,在实际教学中,更常见的是强调“商不变的性质”,即被除数和除数同时乘以或除以同一个非零数,商不变,但考虑到关键词的全面性,这里仍将其纳入讨论范围。
解释: 减法和除法的性质是数学运算中的重要规律,它们展示了运算的逆运算关系和简化计算的途径,掌握这些性质有助于提高学生的运算能力和解题技巧。
落实方法:
- 直观演示与操作:利用实物或图形来展示减法和除法的性质,帮助学生直观理解。
- 分步练习与对比:设计分步计算的练习题,并通过对比不同运算方式的结果来加深学生对性质的理解。
- 应用题与实践活动:创设生活情境或组织实践活动,让学生在解决实际问题中运用减法和除法的性质。
- 强调逆运算关系:通过具体例子来强调减法和除法的逆运算关系,帮助学生理解并掌握这一重要性质。
- 综合练习与测试:设计综合练习题和测试卷来检验学生对减法和除法性质的理解与掌握情况。
- 鼓励自主探索与合作交流:鼓励学生自主探索减法和除法性质的规律并分享自己的发现;同时组织学生进行合作交流以深化对性质的理解和运用能力。
转载请注明出处: 李小帅
本文的链接地址: https://lxs.asia/?post=246
-

体彩超级大乐透中奖规则详细解答、解释与落实
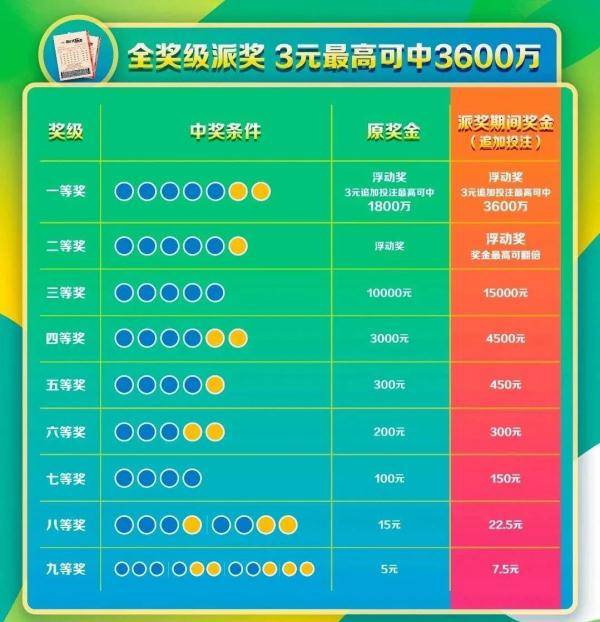
体彩超级大乐透中奖规则详细解答与落实体彩超级大乐透作为中国体育彩票的一种重要玩法,自推出以来,因其高额的奖金和独特的玩法规则,吸引了众多彩民的关注与参与,对于不少新手彩民而言,体彩超级大乐透的中奖规则可能显得较为复杂,本文将详细解答体彩超级大乐透的中奖规则,并进行深入解释与落实,帮助彩民更好地理解和参与这一游戏……
4天前
-

王中王493333特马王中王,警惕虚假宣传、全面解答
警惕虚假宣传:揭开“王中王493333特马王中王”的神秘面纱在当今社会,随着互联网的飞速发展,各种信息如潮水般涌来,其中不乏一些夸大其词、甚至虚假的宣传,“王中王493333特马王中王”这一关键词在网络上频繁出现,引起了广泛关注,这背后隐藏着怎样的真相?本文旨在全面解答这一关键词背后的虚假宣传问题,帮助读者擦亮……
5天前
-

太空望远镜发现迄今为止地外行星上存在生命的最有力证据
发现迄今为止地外行星上存在生命的最有力证据在浩瀚无垠的宇宙中,人类对地外生命的探索从未停歇,随着科技的进步,太空望远镜作为探索宇宙奥秘的重要工具,不断给我们带来新的发现和突破,一项由国际太空机构合作的研究项目,通过先进的太空望远镜观测数据,发现了迄今为止地外行星上存在生命的最有力证据,这一发现不仅震撼了科学界……
5天前
-

2025新澳门正版免费正题的警惕虚假宣传-全面释义、解释与落实
警惕2025新澳门正版免费正题的虚假宣传:全面释义、解释与落实在信息时代,网络上的各种信息如潮水般涌来,其中不乏虚假的宣传,特别是针对“2025新澳门正版免费正题”这一关键词,网络上出现了大量打着“免费”、“正版”旗号的虚假广告,诱导用户点击下载,从而获取不正当利益,本文旨在全面释义这一现象,解释其背后的原因……
5天前
-

2025新澳天天开彩大全请全面释义、解释与落实
2025新澳天天开彩大全:全面释义、解释与落实随着科技的飞速发展和社会的不断进步,彩票行业也在不断创新与变革之中,2025年新澳天天开彩大全作为彩票行业的一项重要创新举措,旨在通过科技手段提升彩票的透明度、公平性和便捷性,为彩民提供更加丰富多彩、安全可靠的购彩体验,本文将从全面释义、解释与落实三个方面,深入探讨……
5天前
-

2025新澳门原料免费大全1688请全面释义、解释与落实
探索2025新澳门原料免费大全1688:全面释义、解释与落实随着科技的飞速发展和全球化的深入,原料市场正经历着前所未有的变革,2025年,对于澳门而言,是一个充满机遇与挑战并存的关键节点,在这一年里,澳门提出了“新澳门原料免费大全1688”的宏伟蓝图,旨在通过优化资源配置、促进产业升级、加强国际合作,实现原料市……
5天前
-

2025港澳资料免费大全详细解答、解释与落实
2025港澳资料免费大全:详细解答、解释与落实随着2025年的临近,关于港澳地区的发展规划、政策解读及其实施细节成为社会关注的焦点,本文旨在提供一个全面而详细的解答,解释2025年港澳资料免费大全的核心内容,并探讨其如何得到有效落实,以促进港澳地区的持续繁荣与稳定,2025港澳资料免费大全概览2025港澳资料免……
5天前
-

博尔特刷刀体质下载,警惕虚假宣传-全面释义、解释与落实
警惕虚假宣传:全面解析博尔特刷刀体质下载背后的真相在当今信息爆炸的时代,网络上的各种广告和推广信息层出不穷,其中不乏夸大其词甚至虚假宣传的内容,“博尔特刷刀体质下载”这一关键词在网络上引起了广泛关注,不少用户被其所谓的“神奇效果”所吸引,却往往忽视了背后可能隐藏的陷阱,本文旨在全面解析这一现象,提醒公众警惕虚假……
5天前
-

2025年澳门免费资料期期中警惕虚假宣传、全面解答与解释
警惕2025年澳门免费资料期期中的虚假宣传:全面解答与解释在信息时代,网络上的各类资料、信息如潮水般涌来,其中不乏一些打着“免费”旗号的资料宣传,特别是在2025年,随着互联网的普及和社交媒体的发达,关于澳门免费资料的虚假宣传更是层出不穷,这些虚假宣传往往以诱人的标题和承诺吸引用户点击,但实际上却可能隐藏着陷阱……
5天前
-

美运营商T-Mobile将恢复自助SIM卡更换
T-Mobile重启自助SIM卡更换服务:便捷与效率并重的新篇章在数字化时代,移动通信技术的飞速发展不仅改变了我们的沟通方式,也极大地提升了用户体验,作为美国领先的电信运营商之一,T-Mobile一直致力于通过技术创新为用户提供更加灵活、高效的服务,T-Mobile宣布将恢复自助SIM卡更换服务,这一举措不仅标……
5天前









 李小帅
李小帅
最新评论
暂无评论